How to measure the square footage of regular areas to be sodded.
Before ordering sod for your new lawn you must calculate the square footage of sod needed. To make the calculation simple, often this total can be reduced to a series of squares and rectangles. Using the following formula makes the task easy and gives you an accurate count of square feet needed.
-
Square or Rectangle
Formula:
Area = L x W
A = Area
L = Length
W = WidthExample:
A = 90 feet x 50 feet
A = 4,500 square feetThe following illustration reduces the areas to be sodded around the house (A, B, C) and the backyard (D) to rectangles.
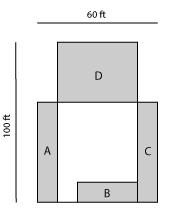
Formula:
Area A = 50’ x 10’ = 500 sq.ft.
Area B = 30’ x 10’ = 300 sq.ft.
Area C = 50’ x 1-‘ = 500 sq.ft.
Area D = 40’ x 30’ = 1200 sq.ft.Example:
Sod Needed: A (500 sq.ft.) + B (300 sq.ft.) + C (500 sq.ft.) + D (1,200 sq.ft.) = 2,500 sq.ft.
How to measure the square footage of irregular areas to be sodded.
Typically, you can reduce any irregularly shaped turf area to one or more geometric figures. You can then calculate the area of each figure and add the areas to obtain the total area. Irregular areas could include a pool, pond, garden, flower bed, tree area and so forth.
-
Ovals, Egg Shapes and Circles
Ovals & Egg Shapes
Formula:
Area = 0.8 L x W
A = Area
L = Length
W = Width at midpointExample:
A = 0.8 x 60 feet x 40 feet
A = 1,920 square feet
(within 5% accuracy)Circles
Formula:
Area =3.14 R2
R = RadiusExample:
A = 3.14 x 30 feet x 30 feet
A = 1,414 square feetThe half circle backyard has a radius of 30 feet. A complete circle would be 302 or 3.14 x 30 ft. x 30 ft. = 2,826 sq.ft. Half would be 1,413 sq.ft.
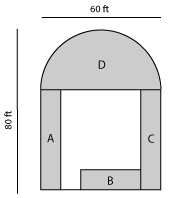
Sod needed: A + B + C (1,300 sq.ft. – see page 1) + D (1,413 sq.ft.) = 2,713 sq.ft.
-
Irregular Shapes
Formula:
Measure the length of the longest axis across the area. Every 10 feet along the length , measure the width of the area at right angles to the length line. Total all widths and multiply by 10.Example:
A = 40 ft. + 30 ft. + 50 ft. x 10
A = 1200 square feet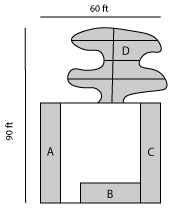
Sod Needed: A + B + C (1,300 sq.ft.) + D (see above) = 2,500 sq.ft.
-
Triangles
Formula:
Area = 0.5 x B x H
A = Area
B = Base
H = HeightExample:
A = 0.5 x 25 ft. x 25 ft. = 312.5 sq.ft. x 2 (triangles) = 625 sq.ft.
A = 625 sq.ft.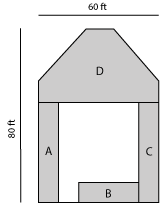
Yard area D (below) is 60ft. x 40ft. = 2,400 sq.ft.
Subtract the 2 triangles (625 sq.ft.)
D = 2,400 sq.ft. – 625 sq.ft. = 1,775 square feetSod Needed: A + B + B (1,300 sq.ft.) + D = 3,075sq.ft.
-
Trapezoid
Formula:
Area = 0.5 x (A + B) x H
A = one parallel side
B = second parallel side
H = Height perpendicular to two parallel sidesExample:
Area = 0.5 x A + B (100 ft.) x H (30 ft.) = 1,500 sq.ft.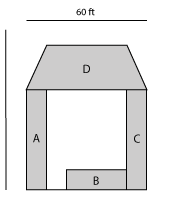
Sod Needed: A + B + C (1,300 sq.ft.) + D = 2,800 sq.ft.
-
Unusual Shapes
Formula:
Divide area into sections of regular geometric shapes, calculate area of individual sections, then totalExample:
Triangle 0.5 x B (15ft.) x H (30 ft.) = 225 sq.ft.
Rectangle 30 ft. x 45 ft. = 1,350 sq.ft.
Circle (3.14) x 9 x 9 = 258 sq.ft. + 2 = 127 sq.ft.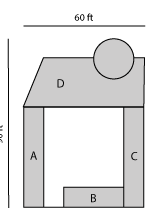
Sod Needed: 225 sq.ft. + 1,350 sq.ft. + 127 sq.ft. = 1,702 sq.ft.
